Number factor problem¶
We have a function
public int waysToGetN(int n)
if(n == 0 || n == 1 || n == 2) // {}, {1}, {1,1} base cases
return 1
if(n == 3)
return 2 //{1,1,1}, {3}
int subtract1 = waysToGetN(n-1)
int subtract3 = waysToGetN(n-3)
int subtract4 = waysToGetN(n-4)
return subtract1 + subtract3 + subtract4
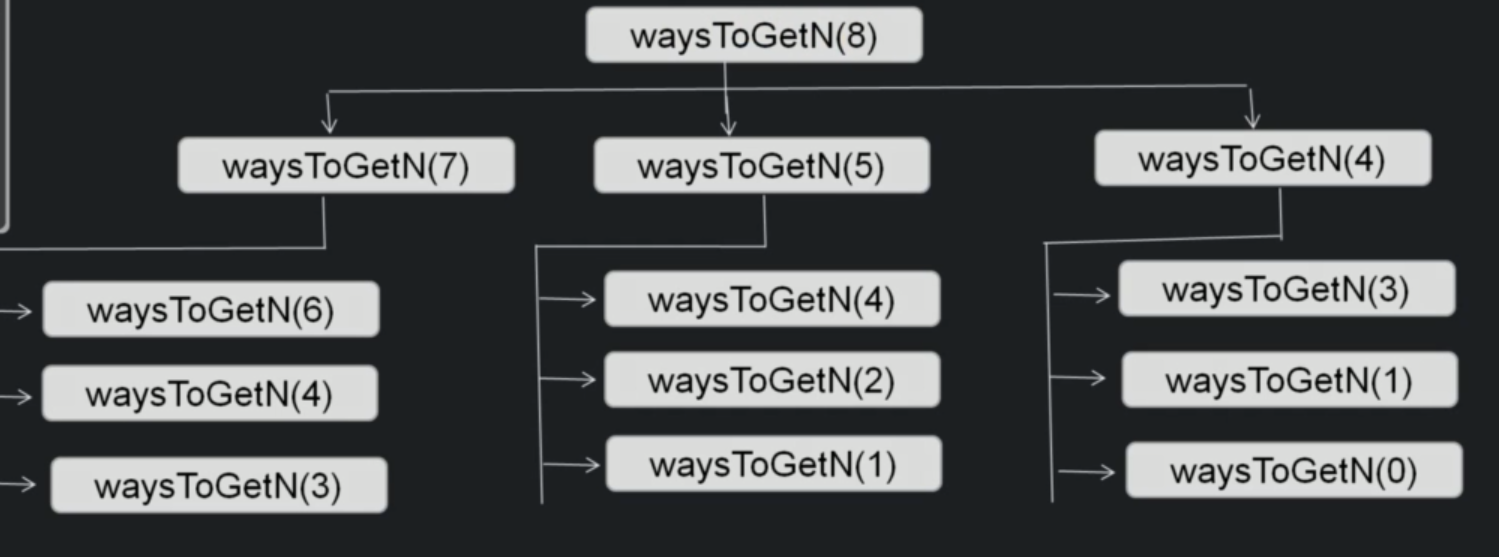
We see that there are problems that we are solving more than once. like waysToGetN(4).
We can use dynamic programming to optimize it.
public int waysToGetN(int n)
return waysToGetN_TopDown(dp, n)
public int waysToGetN_TopDown(int[] dp, int n)
if(n == 0 || n == 1 || n == 2) // {}, {1}, {1,1} base cases
return 1
if(n == 3)
return 2 //{1,1,1}, {3}
if dp[n] == 0
int subtract1 = waysToGetN_TopDown(dp, n - 1)
int subtract3 = waysToGetN_TopDown(dp, n - 3)
int subtract4 = waysToGetN_TopDown(dp, n - 4)
dp[n] = subtract1 + subtract3 + subtract4
return dp[n]