Nubmer factor¶
Problem statement: given N, count the number of ways to express N as sum of 1, 3 and 4.
Example:¶
n = 4 Number of ways = 4 Explanation: Following are the four ways we can express n: {4}, {1,3}, {3,1}, {1,1,1,1}
Example 2¶
n = 5 Number of ways = 6 {4,1}, {1,4}, {3,1,1}, {1,1,3}, {1,1,1,1,1}
Applying magic framework¶
If we would apply the magic framework to this problem, we would see that:
-
The greedy choice is not applicable here.
That is because we can't really tell if we have taken the best sub-solution result - we can't tell if we pick number 1 that is the best pick of all the numbers.
-
It does have an optimal substructure.
We can break down the problem in smaller, similar sub-problems.
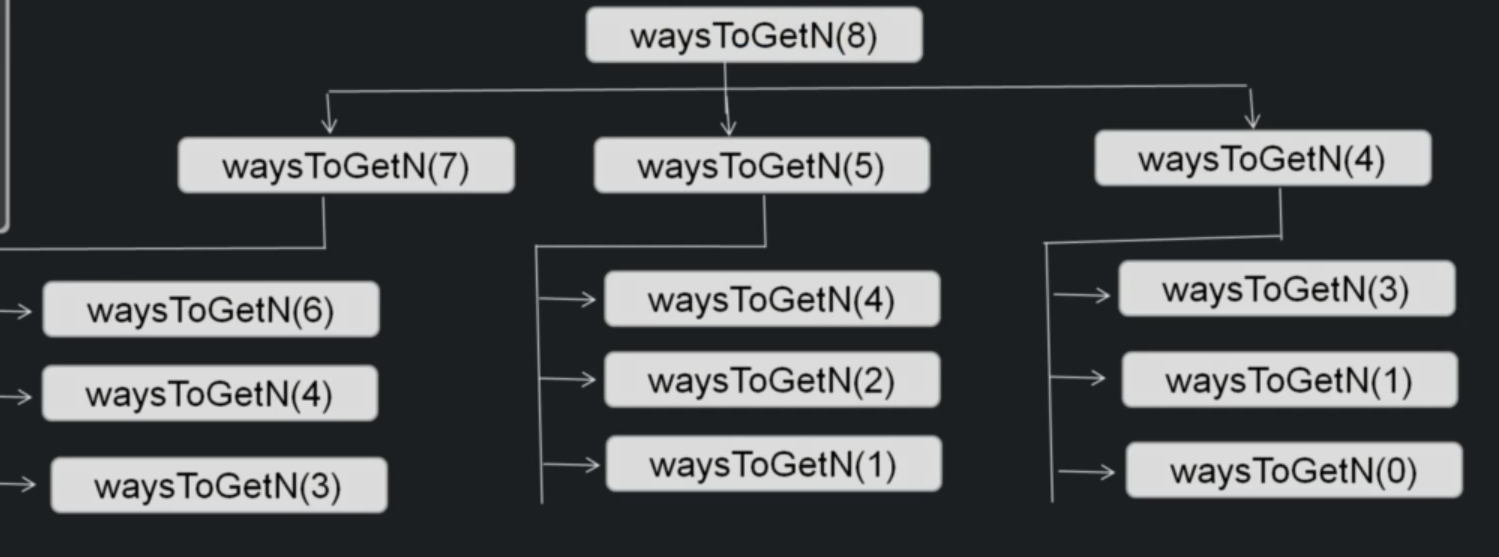
The algorithm¶
public int waysToGetN(int n)
if(n == 0 || n == 1 || n == 2) // {}, {1}, {1,1} base cases
return 1
if(n == 3)
return 2 //{1,1,1}, {3}
int subtract1 = waysToGetN(n-1)
int subtract1 = waysToGetN(n-3)
int subtract1 = waysToGetN(n-4)
return subtract1 + subtract3 + subtract4