What is a graph¶

A graph is a pair of sets (V, E) where V is the set of vertices and E is the set of Edgets, connecting the pairs of vertices.

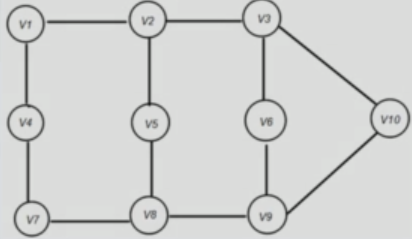
V = {v1, v2, v3, v4, v5,v6, v7, v8, v9, v10}
E = {v1v2, v2v3, v1v4, v4v7, v7v8, v2v5, v5v8, v3v6, v6v9, v8v9, v3v10, v9v10}

One of the use cases of graphs can be that we can use graphs to find shortest paths between points in the graph.

Terminologies¶

Vertices - nodes of the graph
Edges - the arcs that connect pairs of vertices
Unweighted graph - a graph not having a weight associated with any edge
Weighted graph - graph having weight associated to each edge
Undirected graph - graph that is set of vertices connected by edgets, where the edges don't have a direction associated with them.
Directed graph - the edges have direction associated with them
Cyclic graph - a graph having at least one loop
Acyclic graph - without any loops
Tree - A special case of directed acyclick graph (DAG)