What is a binary heap¶

Binary heap is a binary tree, but with some special properties: - Heap property: - value of any given node must be <= value of it's children (min-heap property) - value of any given node must be >= value of it's children (max heap) - Complete tree - All levels are completely filled except possibly the last level and the last level has all keys as left as possible. - This makes binary heap ideal candidate for array implementation.

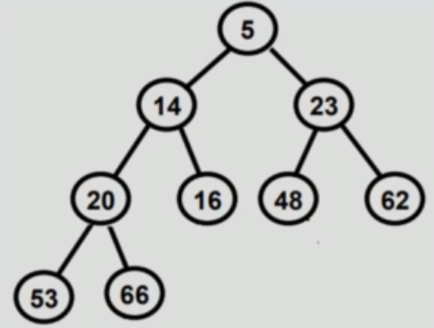
Why learn Binary Heap?¶

There are cases when we want to find min/max number along set of numbers in log(n) time. Also, we want to make sure that inserting additional numbers does not take more than O(log n) time.

Possible solutions: 1. Store numbers in a sorted array. But, when we are going to insert a new number, it will take O(n) time to do that. 2. Store the numbers in a linked list, in a sorted manner, but it will also take O(n) time.

Types of binary heap¶

There are 2 types of binary heap:

• Min heap - if the value of each node is less than or equal to value of both it's children

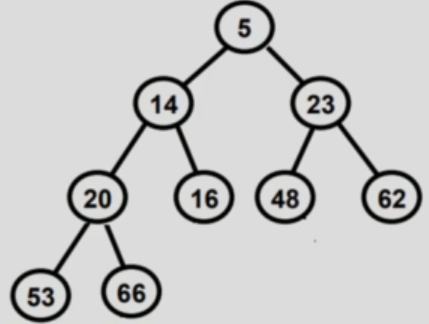
• Max heap - if the value of each node is more than or equal to value of both it's children

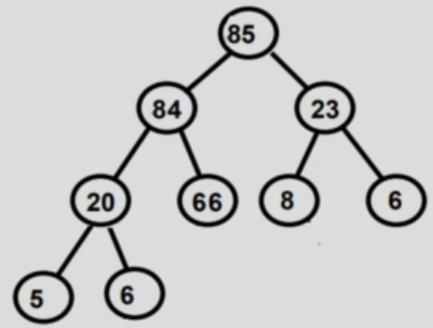
Common operations¶

• Create Heap - creates a blank Array to be used for storing heap
• Peek top of heap - returns min/max from heap
• Extract min/max - extracts min/max from heap, we can extract only this node.
• Size of heap - returns size of the heap
• insert value in heap - insert value in heap
• delete heap - deletes the entire heap