Implementing binary tree with a Linked List
createBinaryTree()
Create an object of Binary Tree class
Time complexity - O(1)
Space complexity - O(1)
preOrderTraversal(root) ---------------- T(n)
if(root == null) -------------- O(1)
return error -------------- O(1)
print root -------------------- O(1)
preOrderTraversal(root.left) -- T(n/2)
preOrderTraversal(root.right) - T(n/2)
Time complexity - O(n)
Space complexity - O(n)
inOrderTraversal(root) ---------------- T(n)
if root == null -------------- O(1)
return error ------------- O(1)
inOrderTraversal(root.left) -- T(n/2)
print root ------------------- O(1)
inOrderTraversal(root.right) - T(n/2)
Time complexity - O(n)
Space complexity - O(n)
postOrderTraversal(root) ---------------- T(n)
if root == null ---------------- O(1)
return error --------------- O(1)
postOrderTraversal(root.left) -- T(n/2)
postOrderTraversal(root.right) - T(n/2)
print root --------------------- O(1)
Time complexity - O(n)
Space complexity - O(n)
levelOrderTraversal(root)
create a queue(Q) -------------------- O(1)
enqueue(root) ------------------------ O(1)
while(queue is not empty) ------------ O(n)
enqueue child of first element --- O(1)
dequeue and print ---------------- O(1)
Time complexity - O(n)
Space complexity - O(n)
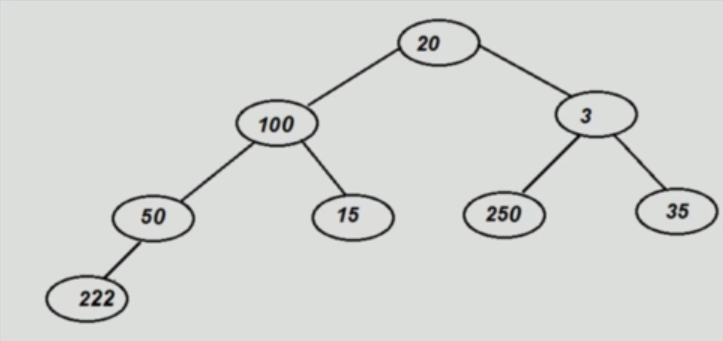

searchTree(value)
if root == null ----------------- O(1)
return error ---------------- O(1)
do a level order traversal ------ O(n)
if value found -------------- O(1)
return true ------------- O(1)
return false -------------------- O(1)
Time complexity - O(n)
Space complexity - O(n)
insertNode():
if root is blank
insert new node at root
else
do a level order traversal and find the first blank space
insert that blank space
Time complexity - O(n)
Space complexity - O(n)
deleteNode()
search for the node to be deleted
find deepest node in the tree
copy deepest node's data in current node
delete deepest node
Time complexity - O(n)
Space complexity - O(n)
DeleteBinaryTree()
root = null
Time complexity - O(1)
Space complexity - O(1)
Time and space complexity
|
Time complexity |
Space complexity |
| create tree |
O(1) |
O(n) |
| insert value |
O(n) |
O(n) |
| delete value |
O(n) |
O(n) |
| search |
O(n) |
O(n) |
| traverse |
O(n) |
O(n) |
| delete tree |
O(1) |
O(1) |

