Circular queues¶
There is a small problem with the linear queues, so a circular queue was created.
The problem arises when using deQueue method leaves a blank cell when it extracts an element, which then becomes unused. When we have a limited space, this is not an optimal usage of the space.
The fix for that is to move all the elements to the start of the array, after executing the deQueue.
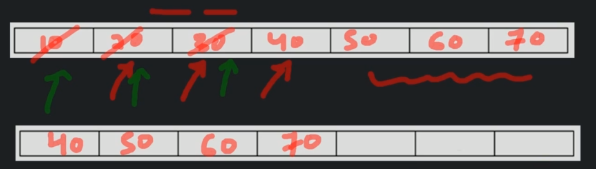
The tradeoff is that when we start moving the elements to the start of the array, the time complexity moves from O(1) to O(n).
To manage this in O(1) time complexity, we can use circular queues, which basically checks, whenever we want to add an element to the queue, and we are already at the end, if there are any elements at the start that are empty and add them there.

createQueue(size)
create a blank array of `size`
initialize topOfQueue, beginingOfQueue to -1
Time complexity O(1)
Space complexity O(n)
enQueue(value)
if queue is full
return error
else if topOfQueue+1 == size
// top at the last cell of array, reset it to first cell
topOfQueue = 0
else
topOfQueue++
arr[topOfQueue] = value
Time complexity O(1)
Space complexity O(1)
deQueue()
if queue is empty
return error
print arr[beginningOfQueue]
if start == topOfQueue // only 1 element
start = topOfQueue = -1
else if start + 1 == size // start has reached end of array
start = 0
else
start ++
Time complexity - O(1)
Space complexity - O(1)
peek()
if queue empty
return error
print arr[beginningOfQueue]
Time complexity - O(1)
Space complexity - O(1)
isQueueEmpty()
if topOfQueue == -1
return true
return false
Time complexity - O(1)
Space complexity - O(1)
isQueueFull()
if topOfQueue + 1 == start // completed a circle, queue is full
return true
else if start == 0 && topOfQueue == size
return true
return false
Time complexity - O(1)
Space complexity - O(1)
deleteQueue()
array = null
Time and space complexity of lineart queue¶
| Time complexity | Space complexity | |
|---|---|---|
| create queue | O(1) | O(n) |
| enqueue | O(1) | O(1) |
| dequeue | O(1) | O(1) |
| peek | O(1) | O(1) |
| isEmpty | O(1) | O(1) |
| isFull | O(1) | O(1) |
| delete queue | O(1) | O(1) |